球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 球の質量基準比表面積(単位質量当たりの表面積) 角錐や円錐の体積や表面積は、円の面積や扇形の面積から導けます。 今回は、円や球の面積・体積、円周・表面積の公式の相互関係を、微分と積分の概念を交えて紹介しました。 これらの式が似ているのは偶然ではなく、その背後に面積の定義式=積分、その変化率=断片長や断面積を表す微分が登場しているのです。 面積や体積の式は、小学校や中学校で覚えなさいと言われますが「体積と表面積の関係」は、簡単に言ってしまうと、「体積が大きくなっても、表面積はそんなに大きくならない」という関係です。 これを具体的に説明してみようと思います。 まず、頭の中に1辺が1センチのサイコロを1つ思い浮かべてみて下さい。 そのサイコロの体積は、もちろん「1立方センチメートル」ですよね。 面積は、というと、6つの面があるのですから、「6平方センチメートル」で

所有面积体积公式大全面积体积公式大全 简笔画图片库
体積 表面積
体積 表面積- 球の表面積 < (2) 2つの比較 (1)(2)より, < 球の表面積 < 方法②:輪切りにする 指針(考え方) この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします.小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題




圆环体积 表面积计算器 9321计算器
縦・横・高さから直方体の体積・表面積を公式を使って計算します。 縦・横・高さを入力し「直方体の体積・表面積を計算」ボタンをクリックすると、直方体の体積・表面積を計算して表示します。 縦の長さ a: 横の長さ b: 高さ c: 縦の長さaが1、横の長さbが2、高さcが3の直方体の体積・表面積 体積 V:6 表面積 S:22 体積・表面積の計算 ・立方体の体積・表面積 ・立方体の体積から1辺 ・立表面積 体積 は、 底面積が円の面積で 高さが だから、 公式が使えないのは、体積より表面積です。 「表面積」とあれば「展開図」、忘れずにいればどれも同じ問題に見えてきますよ。 球(半球)の体積と表面積の求め方 表面積と言われても展開図が書けないのはこの球です。 球だけは公式を使わないと表面積、体積とも中学生は求められません 。 ※ 高校生でも公式を使わないと求められない人はた(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして
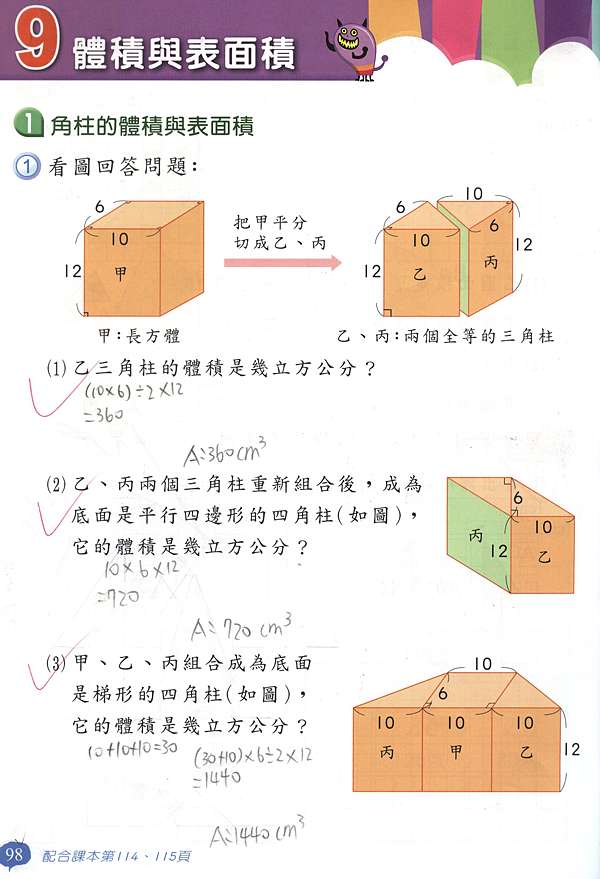
どっちが体積で、どっちが表面積だっけ? というようにごちゃごちゃになっちゃう人も多いです。 そういう人は、 体積と表面積の単位に注目しましょう。 体積の単位には 、 というように3乗がついているよね。 だから、公式にも というように3乗がある。 面積の単位には 、 というように2乗がついているよね。 だから、公式にも というように2乗がある。 このように3乗、2乗を単位と関連付けてお① 立体のすべての面の面積の和を表面積という。 また,側面全体の面積を側面積,1 つの底面の 面積を底面積という。 ②(柱体の体積)=(底面積)×(高さ),(柱体の表面積)=(側面積)+(底面積)×2 問題1右の図の角柱の体積と表面積を求めよ。 解体積 (底面積 )×高さ = 1 2 3 4 *3 6*3=18 cm 3 展開図で考えると,側面全体は長方形で,横の長さは, 3+4+5=12 (cm) 側面積 3 球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4 π r 2 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: 4 3 π r 3
球の表面積の求め方には公式があるんだ。 球の半径をrとすると、その表面積は、 4πr^2 になるよ。 つまり、 4 × 円周率 × 半径 × 半径 ってわけだね。 たとえば、半径30cm のサッカーボールがあったとしよう。 このボールの皮の面積、つまり表面積は、 4 × π × 30 × 30 = 3600π cm^2 になるんだ。 公式にいれて計算するだけでいいんだ。 チョー便利な公式じゃない? 笑 ただ直円柱の体積 そういえばこんな公式でしたね。 ケーキ型をHPに載っているものと違うものを使うにあたって、体積を知りたかった。 計算式は知っているけれどもこうやってあるととっても便利でした。 半径よりは直径のほうがいい気がしますが、普通に 世の中にはいろいろな形の立体があり、それらがどれくらいの大きさなのかを把握するのに「体積」、「表面積」を用います。 立体というだけで、苦手になるお子さまが多くなるのですが、円柱の体積や表面積を求めるには、円の面積や円周の長さの求め方が必要で、さらに苦手なお子さまが多くなります。 ここでしっかりと確認しておきましょう。 円柱の体積・表面積をしっかりマ




圆柱体体积表面积教具圆柱体积比 大部分地区包邮紧贴课本器材与课本同步 博士荣旗舰店 淘优券



圆柱的表面积和体积练习题精选 松鼠文库
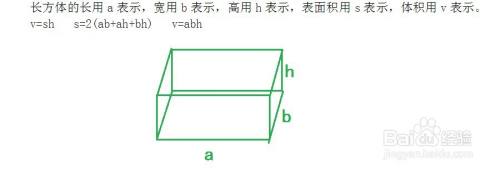
体積・表面積の知識 1立方体と直方体 立方体の体積=1辺×1辺×1辺 立方体の表面積=1辺×1辺×6 直方体の体積=たて×よこ×高さ 2角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい 角すいと円すいの体積=底面積×高さ× 1 3 角すいと円すいの表面積=底面積側面積 4円すいの展開図 側面のおうぎ形の中心角=360°× 底面の半径 母線 底面の半(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして 球の体積の公式はV=4/3πr³ 球の体積を V 、球の半径を r 、円周率を π としたとき、球の体積Vは以下の式で表すことができます。 V=4/3πr³ (球の体積の公式) 球の表面積の公式はS=4πr² 球の表面積を S 、球の半径を r 、円周率を π としたとき、球の表面積Sは以下の式で表すことができます。 S=4πr² (球の表面積の公式) 球の表面積の公式|語呂合わせの覚え方 球の表面積の公式は数




圆柱体积公式和表面积公式是什么 星火网校




盒子表面的秘密 表面積 快樂是自找的 痞客邦
・表面積=地球の約100倍 ・体積=地球の約倍 比較してもピンとこない数値になっていますが、 太陽は、もの凄く大きい天体である事は理解できるはず! 参考: ウィキペディア 太陽は水素ガスが重力によって引きつけられ丸くまとまっている 中まで巨大なガスが充満していて、中心に向かうにつれて超高温・超高圧の状態。 そして、毎秒60億トンの水素が燃えて熱や 球の体積の求め方(公式)の次は、球の表面積の求め方(公式)を学習しましょう。 下の図のように、 半径rの球があるとき、球の表面積は、4πr2となります。 これもまた、球の表面積の公式がなぜ4πr 2 となるのか疑問に思う人もいるでしょう。 しかし、球の体積の公式と同様に、 球の表面積の公式の証明も、学習する必要はありません。 なので、本記事でも球の表面積の公式の ある立体の曲面の面積のことを曲面積、もしくは表面積と呼びます。 まずは曲面積の公式をみてみましょう。 2重積分を用いた曲面積(表面積)公式 2変数関数 z = f ( x, y) ≧ 0 で与えられる立体の曲面の面積 S は S = ∬ D 1 ( ∂ f ∂ x) 2 ( ∂ f ∂ y) 2 d x d y で求めることができる。 ただし、領域 D は立体の底面である。 曲面積の公式の仕組みを少しだけですが解説します。 曲面積を求




正方体的面积怎么算 长方体 正方体的表面积与体积 破锁网



圆环体的体积和表面积怎么算 知乎
半球台の半径と高さから体積と表面積を計算します。 円環体の体積 円環体の体積 円環体(ドーナツ型)の内半径と外半径から体積と表面積を計算します。 楕円体の体積 楕円体の体積 楕円体の3方向の各半軸 から体積と表面積を計算します。V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jinMade with Perfect Video http//googl/iacPmP




球面積計算球 Yxhsa




圆柱体体积公式 圆柱体积和表面积的比较 蓝盟超越网
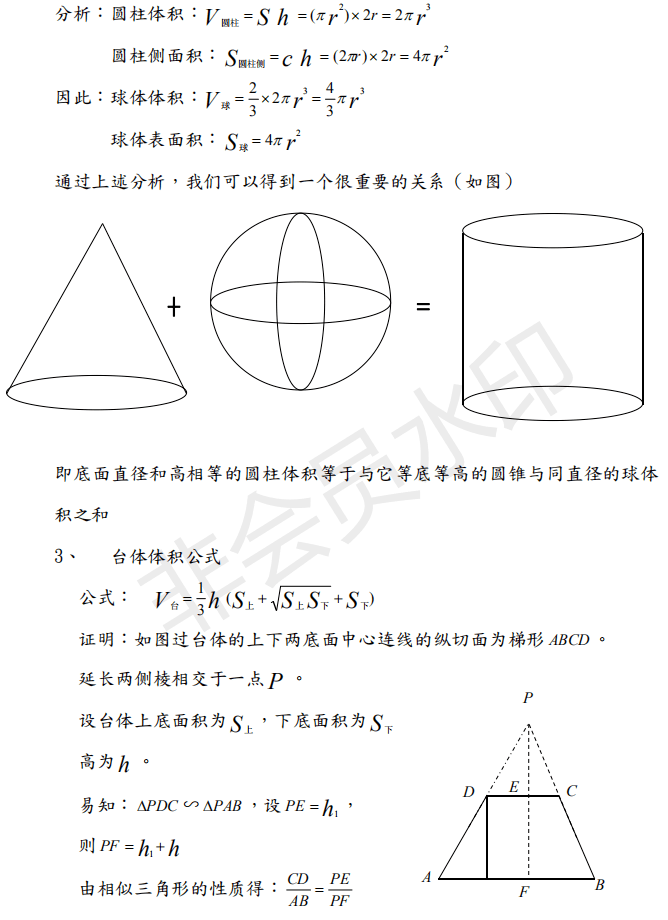
円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S体積: 表面積を求めるためには、底面積と側面積をそれぞれ求める必要がありましたね。 底面の半径は なので 底面積は 円周の長さが であることを利用して 側面積は よって、表面積は となります。 体積は、底面積と高さを掛ければ良いから このように球の体積・表面積の公式は、 公式に半径を代入するだけ で簡単に利用することができます。 実際の試験ではこの内容を発展させて、直方体など他の立体との絡めて体積を求めさせたり、円錐と半円を合わせた立体の表面積を求めさせたりと様々な問題が出題される可能性があります。 どんな問題が出題されたとしても公式を利用することは変わらないので、この記事で球




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫



圆环的体积公式是什么圆形的面积表面积体积公式是什么 学习岛
体積が一定で、表面積が最小の円柱にしたい場合の半径と高さの比をわかりやすく解説してください。 匿名 より 21年8月29日 740 PM This is "球の体積と表面積" by 熊谷一亮 on Vimeo, the home for high quality videos and the people who love them




圆环体积 表面积计算器 9321计算器




简单几何体的表面积与体积 立体几何初步ppt 柱 锥 台的表面积和体积 下载 牛二ppt



體積公式表




柱体体积公式 新人首单立减十元 21年11月 淘宝海外




体积与表面积 西安碑林区新曙光培训学校有限公司



体形面积所有图形的面积体积表面积公式 女士吧




斜棱柱体体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com



五年级下册 图形的表面积和体积练习题一 松鼠文库



立体图形的表面积 第1页 要无忧健康图库



正方體表面積公式




表面积体积常用计算公式 新乡市高服机械股份有限公司




球體的體積與表面積 人人焦點
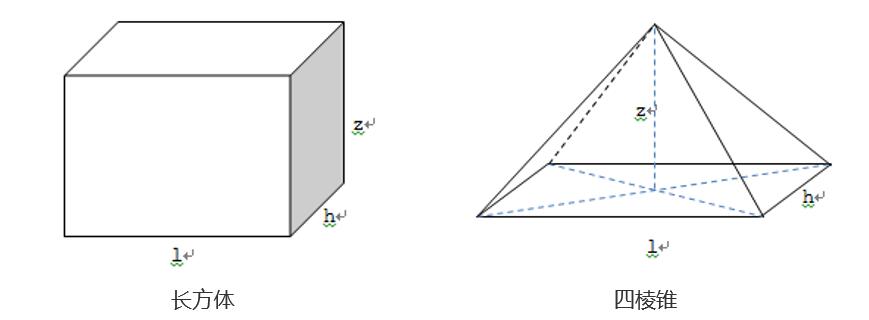



7 2 Sdut Oop 5 计算长方体和四棱锥的表面积和体积 类的继承 10 分 Bless My Head的博客 程序员宝宝 程序员宝宝



球体的表面积体积计算公式是什么 尚书坊




圆锥表面积与体积 圆锥表面积公式 雅风网




长方体正方体表面积体积练习题 Doc 在线文库www Lddoc Cn 在线文库www Lddoc Cn



小学数学立体图形表面积体积公式 图片欣赏中心 急不急图文 Jpjww Com



正方体的表面积和体积公式是什么正方体的表面积和体积公式是怎样的 天奇生活



体积公式大全所有图形的面积体积表面积公式 尚书坊




圆柱体体积表面积 圆锥体体积 圆柱体体积表面积 圆锥体体积图片 价格 品牌 评价和圆柱体体积表面积 圆锥体体积销量排行榜



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社



小学数学奥林匹克竞赛真题精选五年3 长方体体积与表面积 哔哩哔哩 つロ干杯 Bilibili




圆柱的面积公式表面积公式体积公式 大肚妈




考纲考向 简单几何体的体积与表面积
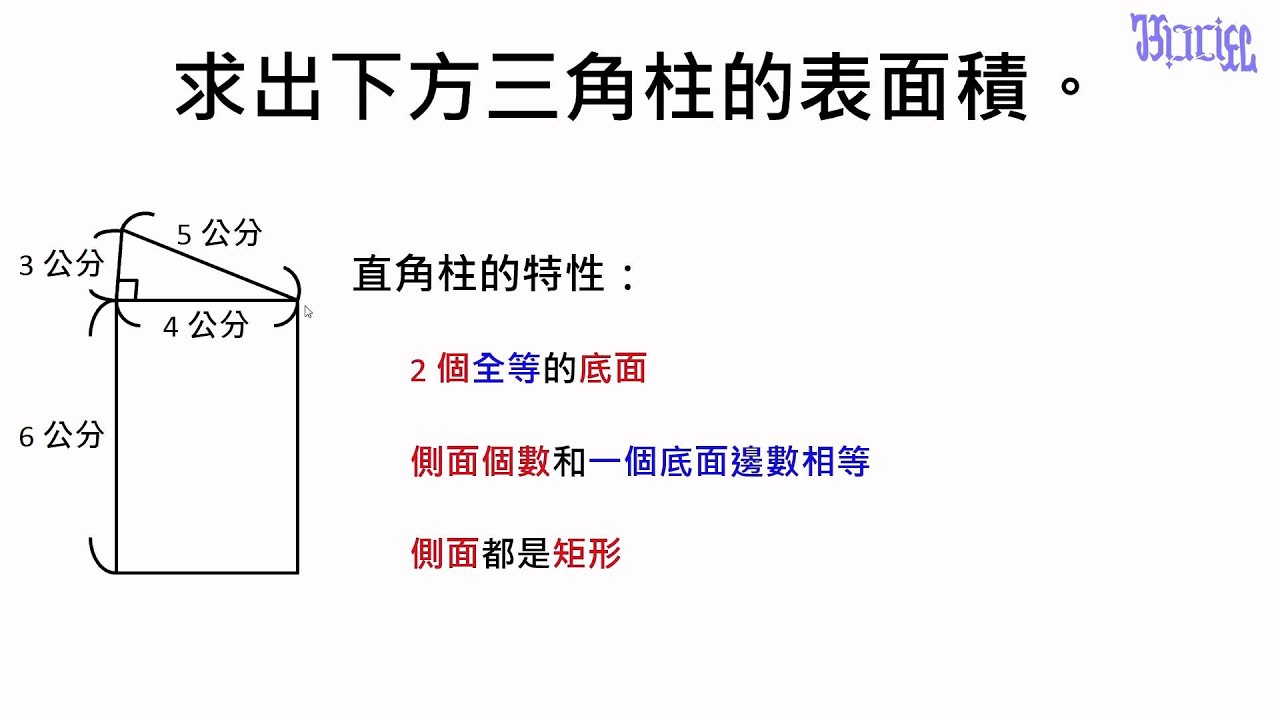



柱體的體積與表面積 03 求出三角柱的表面積 Youtube




周长 面积 表面积和体积 3d动画 Mozaik电子教育与学习




大师一百 高中数学 空间几何体的表面积和体积公式




圆柱体体积表面积教具圆柱体积比 大部分地区包邮紧贴课本器材与课本同步 博士荣旗舰店 淘优券




柱体体积公式 新人首单立减十元 21年11月 淘宝海外




六年级奥数 立体图形的表面积与体积 Doc 三九文库网




柱體表面積柱體表面積公式 Qkaxtw




空间几何体的表面积和体积公式 方法 经典习题 建议大家收藏
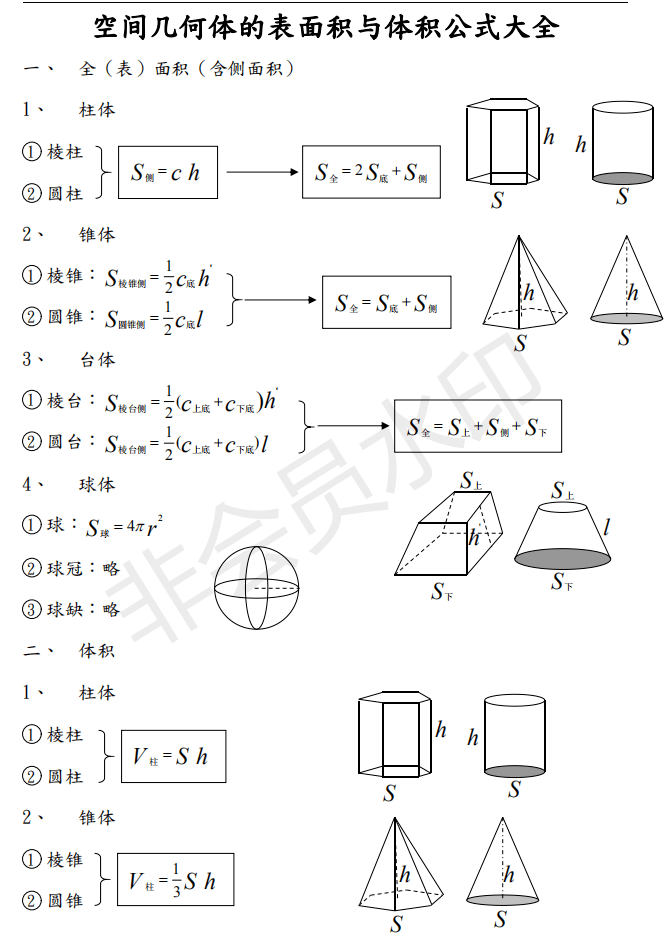



22高三数学第一轮复习 空间几何体的表面积与体积公式大全 整理
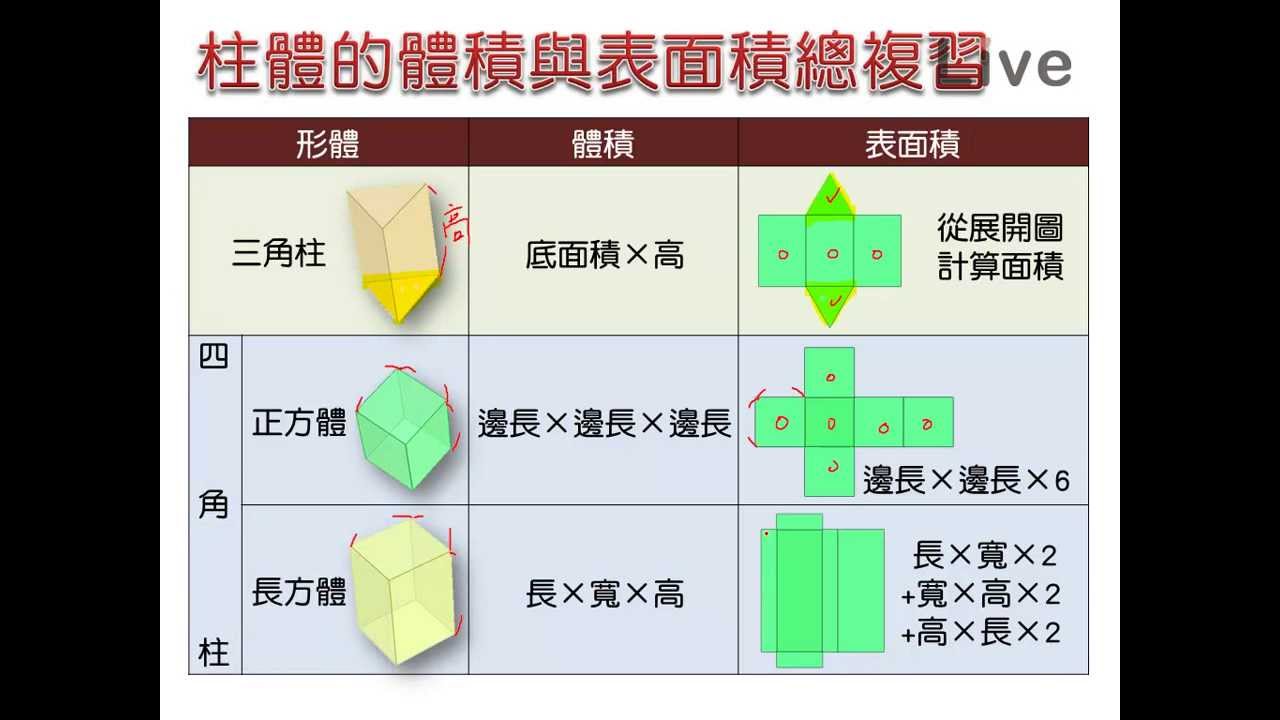



7 國小數學總複習 圖形 體 體積與表面積 觀念 By Live數位國中數學 名師葛倫 Youtube




康軒版六下第三單元形體關係 體積與表面積 Shareclass



看图计算物体的表面积与体积 题目和参考答案 青夏教育精英家教网
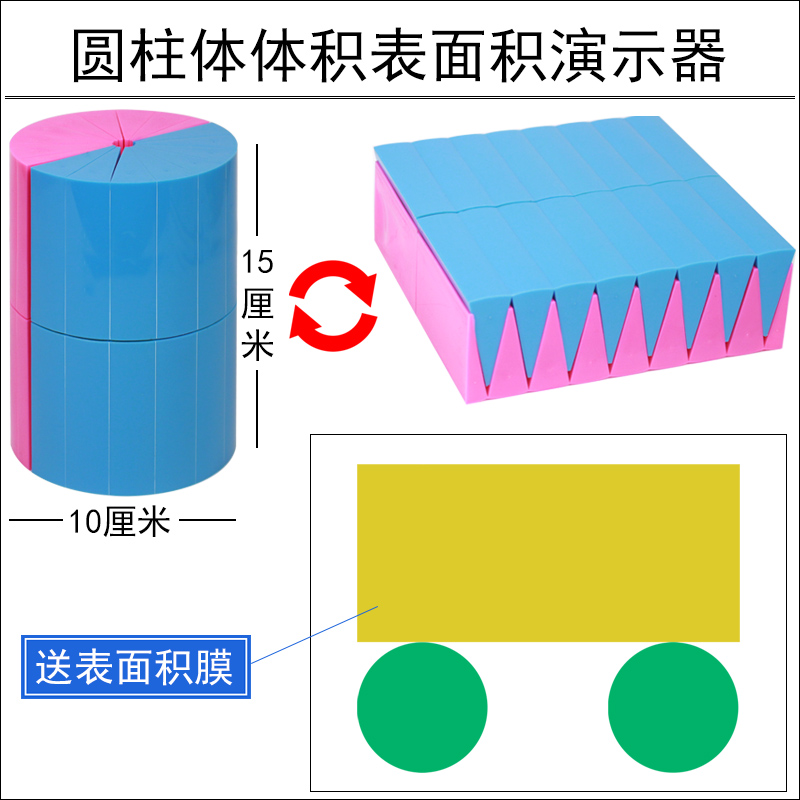



圆柱圆锥体体积推导教具学具体积比6六年级圆柱体体积表面积演示器展开面积计算公式小学生用数学教学模型大号 圆柱体积表面积 送表面积 膜 图片价格品牌报价 京东




圆柱体体积表面积演示器 圆柱体体积表面积演示器图片 价格 品牌 评价和圆柱体体积表面积演示器销量排行榜



立方体平面表面积体积长方体png图片素材免费下载 图片编号 Png素材网




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com




用电子表格求长方体的表面积和体积 百度经验




球體表面積球體 表面積 體積 Vhjk



正方体的表面积与体积计算问题 哔哩哔哩 つロ干杯 Bilibili




球の表面積と体積の公式 数学fun
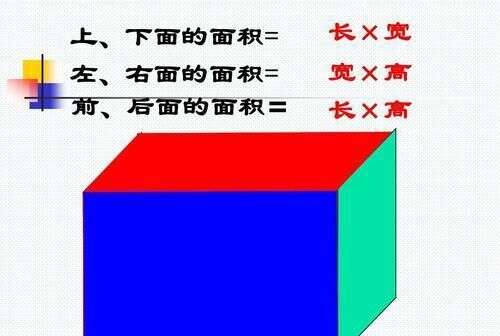



小學數學知識點 長方體與正方體的表面積與體積 楠木軒
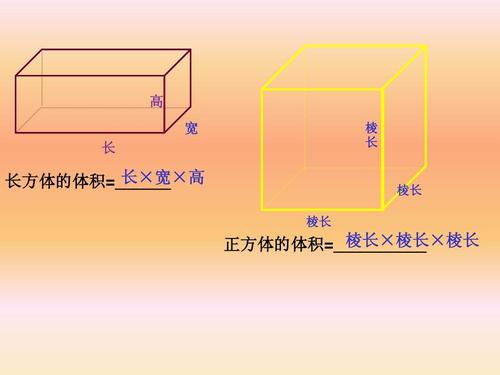



正方体面积计算公式 正方体的体积公式和正方体的表面积公式 作业帮




Ppt 體積與表面積powerpoint Presentation Free Download Id



15柱體表面積數學習作訂正 高以儒 楊老師的部落格 痞客邦




备战高考专题训练 空间几何体的三视图 表面积和体积 附答案 升学 恒艾教育




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clearnote




圆柱体教具立体几何模型体积表面积演示器小学数学教学用具 虎窝淘




体积和表面积 练习 3d动画 Mozaik电子教育与学习




如何从表面积计算立方体的体积 社会 November 21




正方体的表面积公式是什么 长方体和正方体棱长和 表面积 体积计 长方体表面积公式文字 蜂产网




呆哥数学立体几何 表面积与体积 常考例题分析 2 知乎




所有面积体积公式大全面积体积公式大全 简笔画图片库



上新 N文化用品圓柱圓錐體積推導教具小學數學六年級體積教具圓柱體模型學生用體積表面積公式推導學具教學儀器 蝦皮購物




角錐 円錐の体積と表面積の公式 数学fun



球的表面积公式和体积公式是什么 搜狗指南




球表面積計算球的體積 Jlxpis



小学数学中的常见立体体积以及表面积公式有哪些 百度经验




圆环体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




各類幾何體的體積與表面積的計算問題 每日頭條




球的體積求導便是球的表面積 互為逆運算 降維與升維 每日頭條



圆锥表面积公式体积 万图壁纸网



圆台表面积与体积公式 学习岛



22高三数学第一轮复习 空间几何体的表面积与体积公式大全 整理




球的表面积与体积 怎么用微积分证明球的表面积和体积公式 三人行教育网 Www 3rxing Org




初中面积体积公式大全第1页 驾考预约大全



正方体的表面积和体积公式是什么正方体的表面积和体积公式是怎样的 天奇生活




长方体表面积体积立方体png图片素材免费下载 图片编号 Png素材网




面積 表面積 體積的比較 宣宣 2013 の部落格 隨意窩xuite日誌




表面积和体积的区别 解历史




圆柱体体积表面积教具圆柱体积比 大部分地区包邮紧贴课本器材与课本同步 博士荣旗舰店 淘优券




恒一 體積比表面積演示器套裝圓柱體體積表面積演示圓柱圓錐體積比演示器圓周長公式 Yahoo奇摩拍賣



体积公式大全所有图形的面积体积表面积公式 尚书坊



高中数学 体积表面积公式 哔哩哔哩 つロ干杯 Bilibili




體積比表面積演示器套裝圓柱體體積表面積演示圓柱圓錐體積比演示 露天拍賣



长方体正方体的表面积和体积练习题精选 松鼠文库




高中数学必修二经典考题 球的表面积和体积 含答案 三好网




正四面积体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



1




简单几何体的表面积与体积 立体几何初步ppt 球的体积和表面积 下载 牛二ppt



正方体的表面积与体积计算问题 西瓜视频



球的体积和表面积公式怎么算球的表面积和体积 自媒体热点



球體表面積球體 表面積 體積 Vhjk




初中面积体积公式大全第1页 驾考预约大全




立体图形体积和表面积计算的知识梳理



1
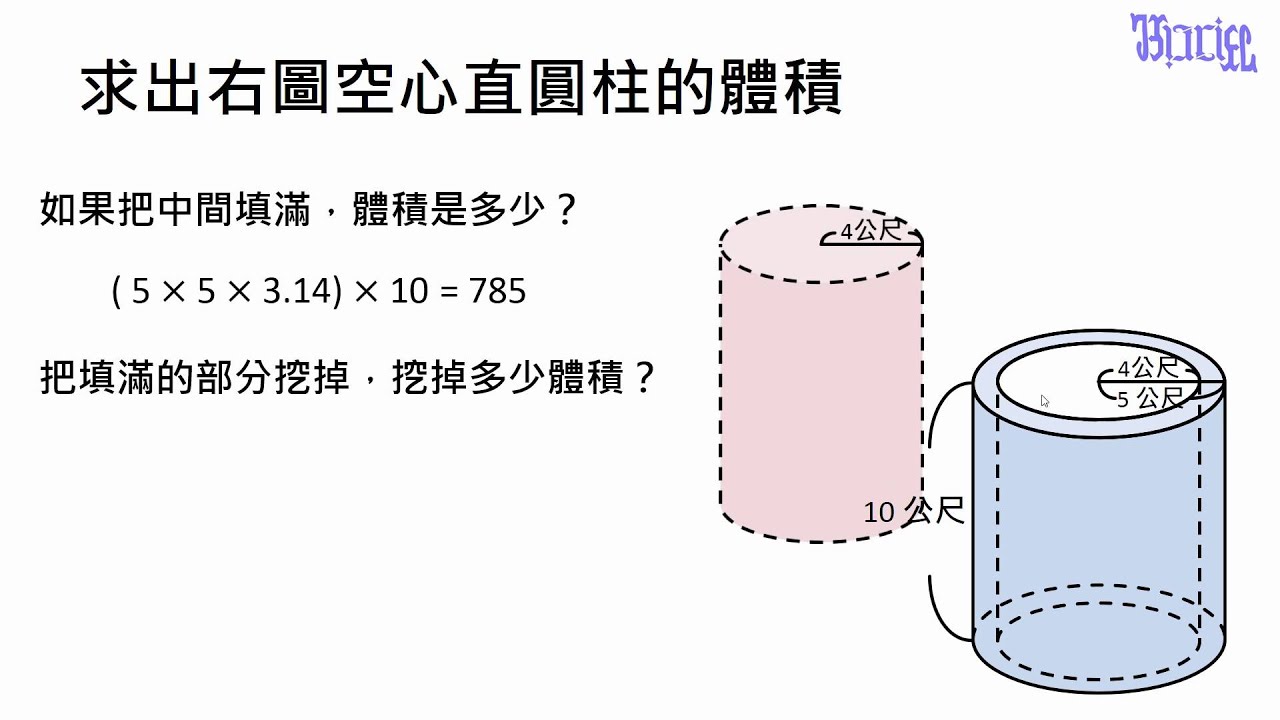



柱體的體積與表面積 21 空心圓柱體的體積 Youtube



图形面积体积公式大全 搜狗图片搜索




15六年级数学下册圆柱表面积 圆锥体积练习题 Doc 文档分享网




体积和表面积计算器安卓下载 安卓版apk 免费下载




圆柱体的体积与表面积 简书



0 件のコメント:
コメントを投稿