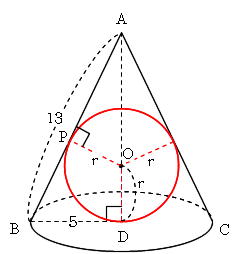
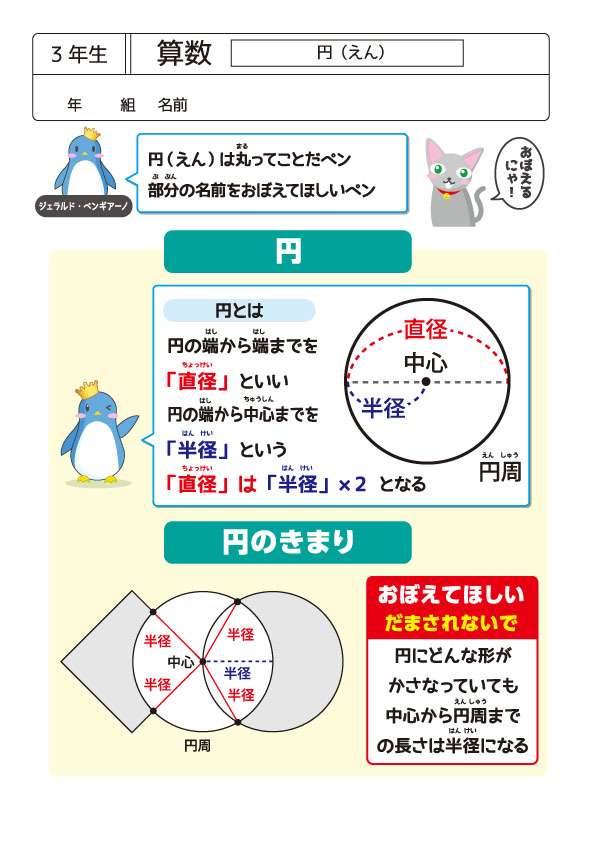
《球の体積の求め方》 球の直径が6cmなので半径は3cm。 求める球の体積を V 、半径を r とすると V = 4 3πr³ より V = 4 3π × 33 = 4 3π × 27 = 36π円の中心,半径,直径の確認や, 円が入った長方形のたてと横の長 さの求め方について想起させる。 箱にバラバラに入った12個の ゼリーを見せ,贈り物にするため にぴったりの箱に並べて入れると いう必然性をもたせる。半径の求め方は? 半径は円の中心から端部までの距離です。下図をみてください。これが半径です。 円の性質を利用した半径の求め方は、いくつもあります。例えば、 直径=半径×2 の関係があります。直径とは円の中心を通る両端部間の距離です。
円錐の底面の半径が3 母線の長さが6です この球の半径の求め方 Yahoo 知恵袋
球の半径の求め方 小学生
球の半径の求め方 小学生-円の半径とは、円の中心から円周上の任意の点を結んだ線の長さです。 半径を最も簡単に求める方法は直径を2で割ることです。 直径がわからなくても、円周 ( C = 2 π r {\displaystyle C=2\pi r} )や円の面積 ( A = π r 2 {\displaystyle A=\pi r^ {2}} )など他の値が与えられ 円の面積 = 半径 × 半径 × 円周率 弧の面積 まず、円の面積を求めて、そのうちの弧の角度分の面積を知りたいので、 弧の面積 = 半径 × 半径 × 円周率 × 弧の角度 ÷ 360 となります。 $$弧の面積=半径 \times 半径 \times 円周率\times \frac{弧の角度}{360}$$



球の体積の半径を求めるのですが どう解けばこうなりますか 4 3pr Yahoo 知恵袋
無料ダウンロード・印刷できる、円と球 円・球の性質、作図、中心・半径・直径 の練習問題プリントです。 円と球の定義や性質を理解し、それを利用した作図や問題の解き方を練習することができ 半径×半径×π×高さ ですので、ここでは、 r×r×π×2r=2πr 3 ですので球の体積は、 2πr 3 ×2/3= 4/3πr 3 ということで、公式がでましたね! 理解できたでしょうか。 以上が、国分寺、小平の個別指導塾、こいがくぼ翼学習塾から、球の体積の求め方でした。5年 学研教育情報資料センター 算数 学習相談 小/算数/5年/図形/ 正多角形と円/理解シート
(ポイント)半径rの球の表面積の公式 半径rの球の表面積をSとすると S=4πr2 (例2)次の球の表面積 を求めなさい。 (解答) 上の図より、球の半径は 6cmなので、 半径rの球の表面積の公 式のrに6を代入すると、 2=144π r=6を代入 答 144πcm2 球の表面積を円周 ÷ π で求めることができます。 円周 : 直径 : π(円周率)= 円周から半径を求める 円周から直径を求める 円周から面積を求める 円の面積から半径を求める 円の面積から直径を求める 円の面積から円周を求める(3)左右おのおののよい方の記録を平均し,キログラム未満は四捨五入する。 4実施上の注意 (1)このテストは,右左の順に行う。 (2)このテストは,同一被測定者に対して2回続けて行わない。
円と球を一体的に,それらの性質の学習が行われる。 続いて,円の面積公式は小学6年,球の体積や表面 積の公式は中学1年で学習されている。小学6年の算 数教科書では,円を単位正方形に分割してその接触球は、接触円と同様な考え方のもので、くぼみに(点や線でなく面で)接触する最大の球です。 接触球が半径rのところでの曲面の曲率Kは、 です。 単位半径の球面の曲率Kは1です。 ふつうの平面は、接触球の半径が無限大 になりますから、その曲率Kは021 球の体積(アルキメデスの求積) ここでは,アルキメデスによる球の体積の求め方について述べる. 力のモーメントを用います.力のモーメントといっても棹秤(さおばかり)の性質です. すなわち,棹ばかりの重さを無視すれば右図でつり合いがとれていれば




マスマスプラス Vol 65 18年秋冬号




中学1年生 数学 無料問題集 球の表面積 おかわりドリル
Scipursuit 体積の求め方 球 球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。 球の体積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは どうも!taraです! 最近暑くなってきましたね 勘弁してほしいものです(笑) って余談は置いておいて、、、 突然ですが、問題です! この図形の表面積を求めてください。 どうでしょう一部が欠けた球の体積 こういうサイトを探していました。 助かりました。 液体接触角の滴定量計測。 今まで表計算ソフトを使って手入力計算していましたが、偶然こちらのサイトを見つけました。 もっと早く見つければよかったです。 超音波




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
正八面体の体積、表面積、外接球の半径、内接球の半径 正四面体の高さと体積の求め方 図形の面積を求める公式たち19個 円の面積を積分で計算する2通りの方法 楕円に関する公式まとめ 双曲線に関する公式まとめ 台形の重心を求める公式と導出⑴ 半径4cmの円 半径 × 半径 × 314 = 円の面積 式 答え ⑵ 半径8cmの円 式 答え ⑶ 直径14cmの円 直径 ÷ 2 = 半径 式 半径 × 半径 × 314 = 円の面積 答え ⑷ 直径18cmの円 式 答え チャレンジシート② きほん 4×4×314=5024 5024㎠ ㎠ 4㎝中2数学1次関数による面積の求め方を解説! 中学生の勉強方法 1993 中1数学反比例の式と性質、グラフについて簡単に解説します! 中学生の勉強方法 515 中3数学二次方程式の練習問題にチャレンジ!(解説あり)




すきるまドリル 小学3年生 算数 円と球 無料学習プリント すきるまドリル 無料学習プリント




円錐 球 円柱の体積比を求めよ 勉強 Youtube スタディチューブ
(21)面積の求め方のくふう(1) 動画 小学校5年生2学期 教師向けコメント 台形の面積を既習の平行四辺形の求積公式を用いて求めることができることをアニメーションから理解する。それをもとに台形の面積の求め方を考えさせる。球の体積の考え方の例 -πr³ 球の表面積の考え方の例 4πr² 4 3 円がぴったり 入る円柱 円がぴったり 入る円柱 球の直径と等しい長さの半径をもつ円になった 円の面積=π(2r)² (rは球の半径) =4πr² 球の表面積=円柱の側面積→円柱の側面積を求める球の体積の解説 球の体積は 4/3×円周率×半径×半径×半径=体積 で求めることができます。円周率をπ、半径をr、体積をVとすると、 V=4/3πr 3 となります。 球の体積を求める公式
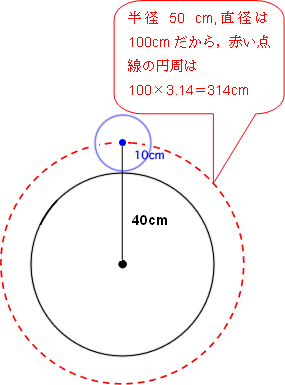



円のまわりをまわる円 算数の教え上手 学びの場 Com




小3 円 円の半径と直径 日本語版 Youtube
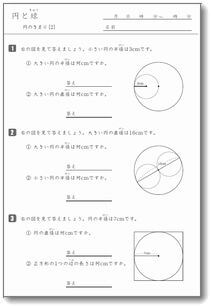
4 × π × 半径 × 半径 × 半径 ÷ 3 で求めることができます。 半径 (r) : 体積 : 小数第4位四捨五入 π(円周率)= 半径から球の体積 半径から球の表面積 直径から球の体積 直径から球の表面積 円周から球の体積 円周から球の表面積球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4 π r 2 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: 4 3 π r 3(3) 半径が3cmの球の直径は cmです。 (4) 球の切り口の形は、いつも になります。 (5) 球の切り口が一番大きくなるのは、球を に切ったとき です。 2 コンパスを使って、次の円をかきなさい。 (1) 半径が2cmの円 (2) 直径が3cmの円 3 答え




球の体積 表面積の求め方 公式 小学生 中学生の勉強




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
感的に求める方法について整理しておきたい。 出発点は、まず円周率である。円周率は、直径に対する円周の比で定義される。数学の 場合、直径というものはあまり使用頻度の高い語彙ではなく、むしろ、半径と絡めた方が本 質的かもしれない。め 球の直径は,球を半分 ㎝ 全 ・ に切ったとき,切り口 体 拡 は一番大きくなるので,ここが直径です。 げ 直径は,16÷4=4で4㎝です。 る ・直径が分かったから,箱のたても求められ ます。の近似値を求めるときに用いられる。 O xm rm x >r のとき 半径x の球面にガウスの法則を適 用すると、 よって、 2 0 4 x EQ 2 0 1 4 E Q x O xm rm 球内の点につ いては、その 点の電界を与 える電荷は、 その点を通る 半径x の同心 QQxr 33 23 00 11 44 E QQx x r x



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
S S S の関係式 S = 1 2 r ( a b c) S=\dfrac {1} {2}r (abc) S = 21 r(a b c) の3次元バージョンです。 内接球の半径,表面積,体積のうち2つ分かれば残りの1つも分かる という公式ですが,ほとんどの場合表面積と体積から内接球の半径を求めることになります3年算数円と球 (1)わかる教え方コンパスの使い方 ①円や球の共通の性質の理解 ②円のかきかたとコンパスの使い方 ③円や球の中心・半径・直径の意味 ④円を使ったいろいろな模様づくりの楽しさ正距方位図法(半径πの円盤→全球) N次元球の表面積と体積の求め方。 こちらでで触れたガンマ関数(Γ Function)の応用例。 Python演算処理階乗と順列と組み合わせ 正直私にとってはパラダイムシフ




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題



球の体積の求め方を簡単に小学生でもわかるように解説をお願いします Yahoo 知恵袋
半径rの球の体積を求める公式は、次のようになります。 πは円周率 (=)です。 球の体積は、半径rの3乗に比例していくということですね! ここで紹介した求め方は、2つとも重要な公式ですのでしっかり覚えるようにしましょう。 球の表面積の公式 S = 4 π r 2 球の体積の公式 V = 4 3 π r 3 チェック! 他にも面積、体積の公式リストがあります。 正多面体の公式一覧《面積と体積》5種類球の表面積 球の表面積 = 半径×半径×4×314 この公式を,パップス・ギュルダンの定理を利用して,小学生レベルで導いてみます。 パップス・ギュルダンの定理による表面積の考え方 回転させたい図形を, (とても細い)針金でできていると考える




円 正方形 球を描画してみる Wolfram Alphaを使って数学を勉強しよう



三角錐に内接する球の半径の求め方 こんにちは中学三年ですが Yahoo 知恵袋
半径 求め 方 円の方程式中心の座標と半径の求め方を解説! 数スタ 内接円の半径の求め方!楽に求める時間の節約術とは?|高校 球の半径を求める 3つの方法 wikiHow おうぎ形半径の求め方は?問題を使って徹底解説! 数スタ;




円の面積 円周の求め方 公式 小学生 中学生の勉強




Python演算処理 半径 直径 円周長 円の面積 球の表面積 球の体積の計算上の往復 Qiita




円の半けいを求めよう 家庭学習レシピ




円の面積 円周の求め方 公式 小学生 中学生の勉強
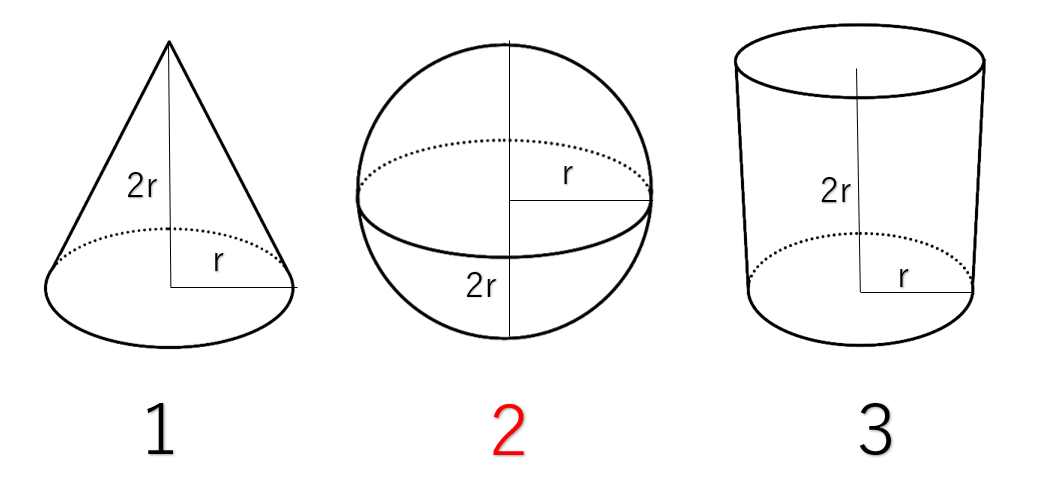



中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾
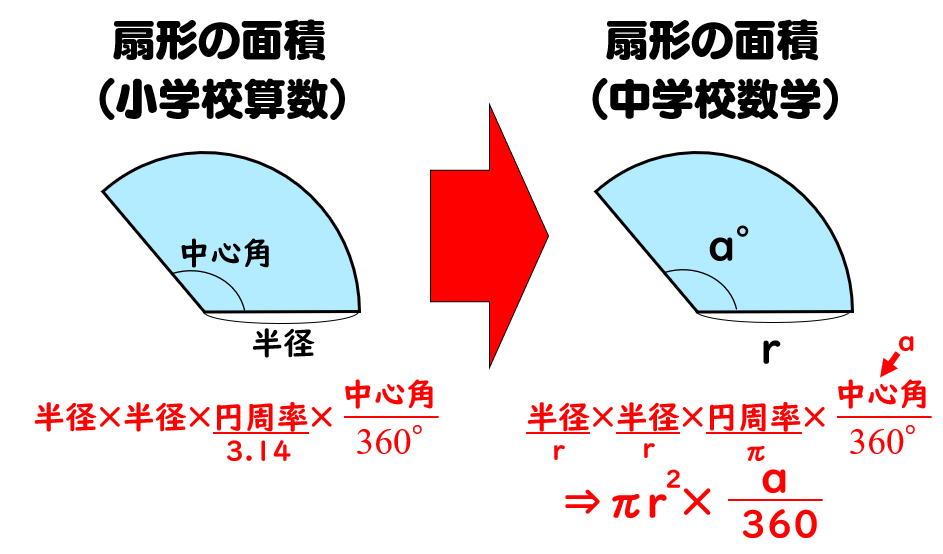



円 扇形 の面積 周や弧の長さの公式 数学fun



円と球プリント ぷりんときっず



働きアリ December 09
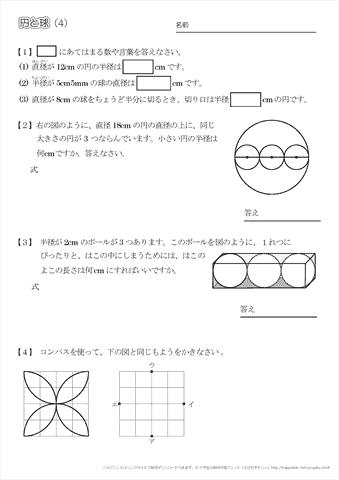



小学3年生の算数 円と球 練習問題プリント ちびむすドリル 小学生
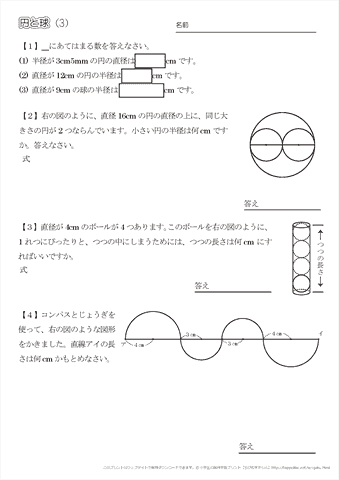



小学3年生の算数 円と球 練習問題プリント ちびむすドリル 小学生




球の半径を求める 3つの方法 Wikihow
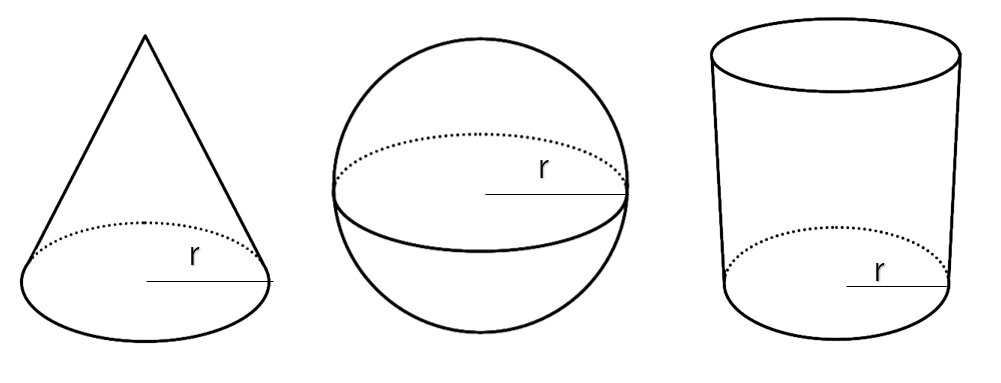



中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾
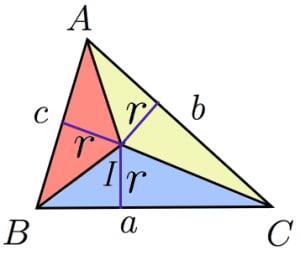



内接球の半径を求める一般的な公式 高校数学の美しい物語




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




この問題の解き方が分かりません 答えは1cmだそうです Clear
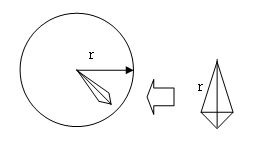



球の計算 もう一度やり直しの算数 数学
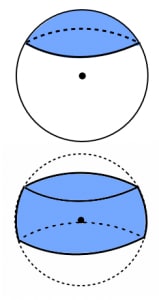



球欠 球台の体積と球冠 球帯の表面積 高校数学の美しい物語
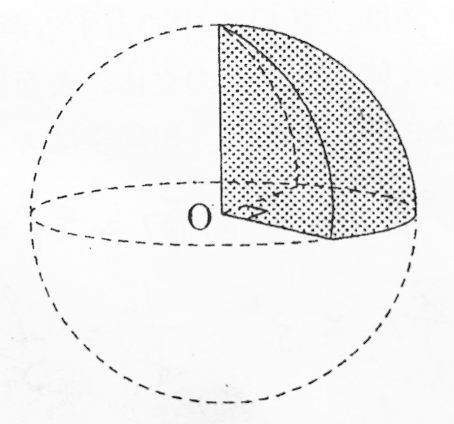



球の問題 苦手な数学を簡単に




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題
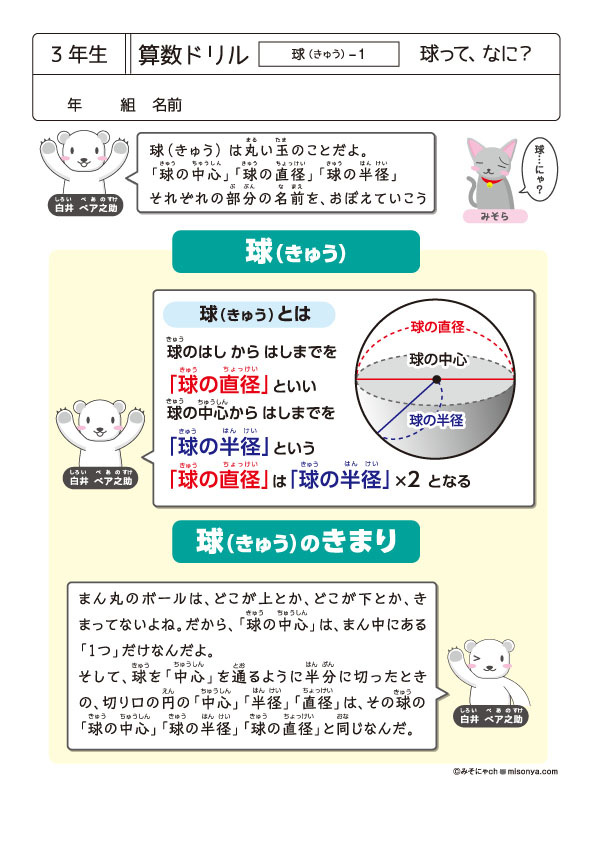



無料の学習プリント 小学3年生の算数ドリル 球 みそにゃch




おうぎ形 注意 周りの長さを求める公式を解説 数スタ



Www Pref Fukushima Lg Jp Uploaded Attachment Pdf




中学1年生 数学 無料問題集 球の表面積 おかわりドリル



Math 円すいの展開図の中心角と母線 半径 小学生 働きアリ



下の円すいの底面の半径の求め方どうやって 求めれば良いのですか Yahoo 知恵袋




半径 求め 方 ニスヌーピー 壁紙




球の体積と表面積 公式と計算問題と証明 Irohabook



円錐の底面の半径が3 母線の長さが6です この球の半径の求め方 Yahoo 知恵袋




小5 複雑な立体の体積 直方体 日本語版 Youtube



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




小3 算数 小3 9 球について Youtube




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく
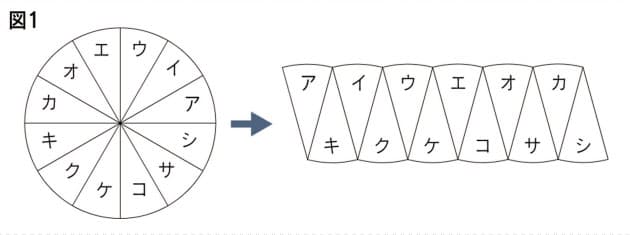



子供に説明できる 円の面積の公式 の証明 Nikkei Style




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




円の面積 円周の求め方 公式 小学生 中学生の勉強




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく




球の計算 もう一度やり直しの算数 数学




円の面積 算数用語集




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく
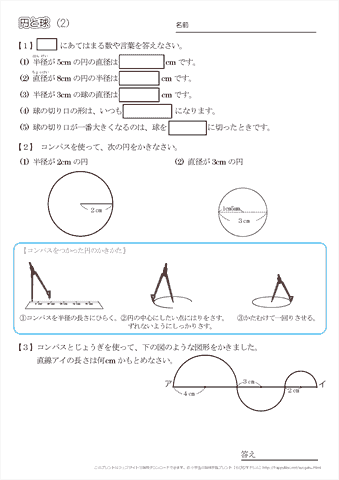



小学3年生の算数 円と球 練習問題プリント ちびむすドリル 小学生
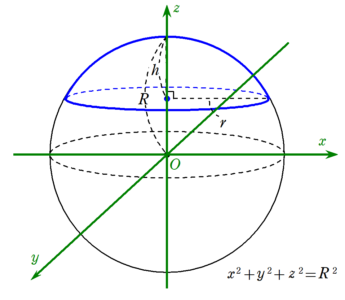



球欠と球冠 Fukusukeの数学めも




球の表面積と体積の公式 数学fun




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




円周の求め方と円の面積について アタリマエ




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



無料の学習プリント 小学3年生の算数 円 みそにゃch




球の表面積と体積の公式 数学fun



小学3年生向けの円と球について学ぶ基本問題




球の体積と表面積 Youtube




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館




球の半径を求める 3つの方法 Wikihow
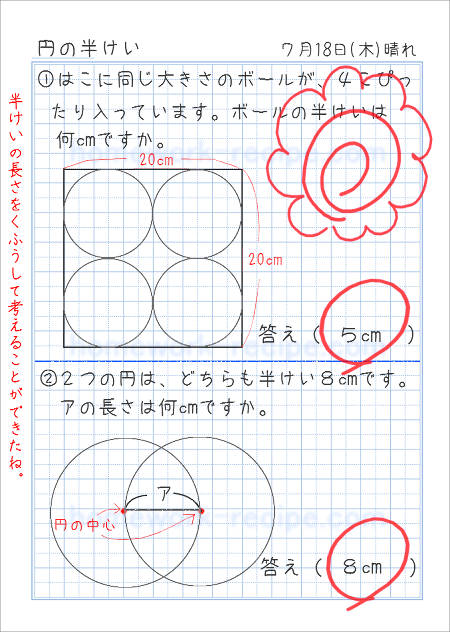



円の半けいを求めよう 家庭学習レシピ



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス
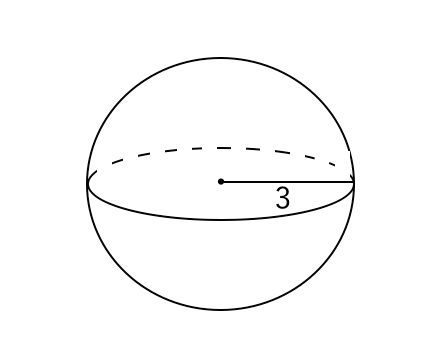



球の表面積と体積の求め方 苦手な数学を簡単に




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の体積の半径を求めるのですが どう解けばこうなりますか 4 3pr Yahoo 知恵袋




中1 数学 6 5 球の体積 表面積 Youtube



円錐とそれに内接する球の表面積比と体積比について 久保塾 今治市の学習塾




球の半径を求める 3つの方法 Wikihow
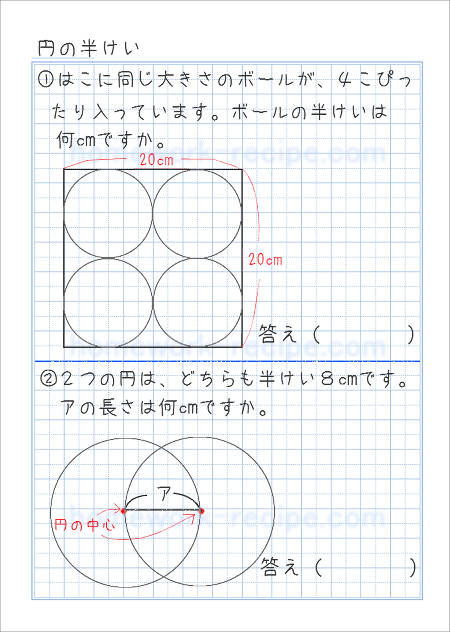



円の半けいを求めよう 家庭学習レシピ



1
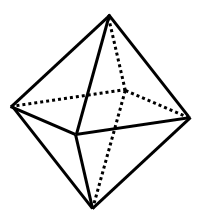



正八面体の体積 表面積 外接球の半径 内接球の半径 具体例で学ぶ数学
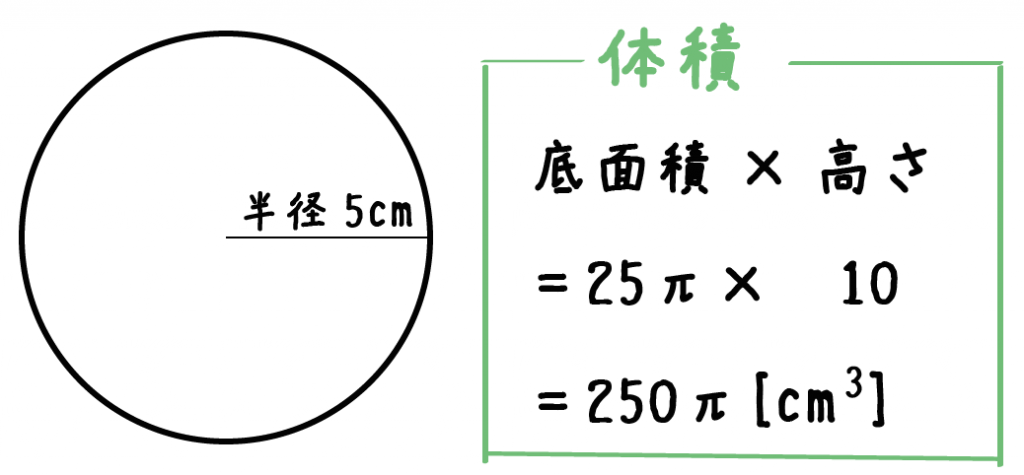



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円 扇形 の面積 周や弧の長さの公式 数学fun




直径から円周の長さの求め方を解説 小学校 中学校でのそれぞれの計算方法は 数スタ




円周の求め方 公式と計算例




立体に内接する球などの問題 無料で使える中学学習プリント




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




球の体積と表面積を積分で証明 高校数学の美しい物語




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題
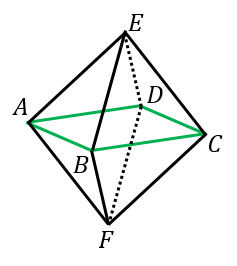



正八面体の体積 表面積 外接球の半径 内接球の半径 具体例で学ぶ数学




小学3年生の算数 円と球 練習問題プリント ちびむすドリル 小学生



1




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾



1




球の表面積と体積の公式 数学fun



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




円柱の体積の求め方 公式 小学生 中学生の勉強




体積 表面積まとめ記事 いろいろな図形の求め方を一気に学べる 高校生向け受験応援メディア 受験のミカタ



3年算数円と球 1 わかる教え方コンパスの使い方



Q Tbn And9gcql0ibk7gneuj9pxmw5ccrcpdqnccuicv0uf U6yiif5myivzfe Usqp Cau
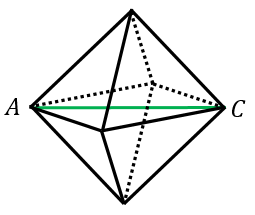



正八面体の体積 表面積 外接球の半径 内接球の半径 具体例で学ぶ数学




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト




球の半径を求める 3つの方法 Wikihow



Www Pref Kochi Lg Jp Soshiki Files File 1 Pdf




表面積の求め方 計算公式一覧



0 件のコメント:
コメントを投稿